1. 引 言

传统的配料皮带秤系统通常采用 PID(  比例- 积分- 微分) 控制器来整定各参数, 在误差较小的范围内 PID 控制算法具有一定的优越性。但是在实际运行当中, 配料皮带秤系统的准确度会受到各种因素的影响, 这些往往使得系统误差不稳定, 动态特性不理想, 无法达到预期的控制效果。

本文提出了基于模糊 PID 控制器的配料皮带秤系统, 将模糊控制技术与传统的 PID 控制技术结合起来共同应用于系统的调节当中, 大大提高了系统抗外部干扰和适应内部参数变化的鲁棒性有效地解决了误差不稳定、动态特性不理想的问题。

2. 系统组成及工作原理

配料皮带秤系统一般由 PLC 上位机、变频器、振动给料机、配料皮带、主皮带、仪表等部件组成, 在配方给定的情况下, 仪表可以独立对配比流量实施闭环控制和调节, 其中采用模糊 PID 控制算法进行调节, 算法内嵌于仪表当中。以配料系统中的一台皮带秤为例, 控制方框图如图 1 所示。

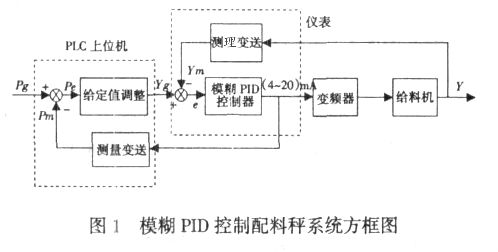
当皮带以一定速度运行时, 称重传感器输出的重量信号和测速传感器输出的速度信号进入仪表, 仪表经运算后得到皮带秤的瞬时流量和累计流量。瞬时流量与仪表内设定的流量值进行比较, 其偏差经模糊 PID 运算后输出 4 mA~20 mA 电流信号。该信号作为调节信号一路送往变频器, 通过改变变频器的频率调节给料机的振动速度, 从而调节物料的流量, 达到配料的目的; 另一路信号送往 PLC 上位机, 上位机根据得到的信息实时调整仪表内的流量给定值。采用模糊 PID 控制器系统可以根据现场不确定的环境变化引起的实际系统误差变化进行实时控制。

3. 模糊 PID 控制器的设计

模糊 PID 控制器是当误差较小时采用传统的PID 控制, 而当误差较大时采用模糊控制, 两种控制方式并行使用, 由比较器进行切换。设 e_g 表示大小偏差量的临界值, 当|e|_g 时, 采用 PID 控制规律; 当|e|>e_g 时, 采用模糊控制规律。模糊 PID 控制器结构图如图 2 所示。

 

 

3.2.2 模糊控制器的实现

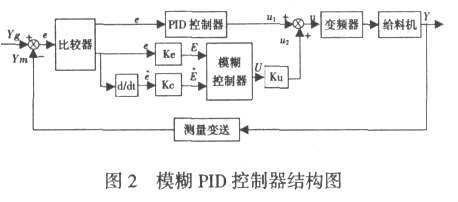
如图 2 所示, 系统中将仪表给定流量 Y_g 与仪表计算得到的瞬时流量 Ym 进行比较, 得到流量偏差e, 如果偏差较大时, 采用模糊控制。偏差 e 经微分后

1. 1. PID 控制器

PID 控制规律为:

得到偏差 e 的变化率e , e 和e 经过模糊量化推理后得到 E,  E 作为模糊控制器的输入, U为控制器的输出。其中 Ke, Kc 为量化因子, 是将输入精确变量 e、e 由基本论域一一映射为相应的模糊集中离散整形值的一个增益, 其取值由两个论域的范围决定; Ku 为输出控制量 U 的比例因子, 由于每次经模糊控制

算法得到的控制量 U 还不能直接控制被控对象, 必U(t)=kpe(t)

(1)须通过一比例因子将其转换到控制对象所能接受的

式中: u (t)——PID 控制器的输出信号;

e(t)——PID 控制器的输入偏差信号;

K_P——比例系数;

T_I——积分时间常数, T_I 越大, 积分作用越弱,

积分时间越长;

T_D——微分时间常数。

PID 控制器采用一般的增量或数字算法, 其参数按常规整定。

1. 2. 模糊控制器
      1. 模糊控制原理

模糊控制是一种基于规则的控制, 它采用语言型控制规则, 将现场操作人员的控制经验或相关专家的知识变成计算机可以接受的控制模型, 让计算机来代替人进行有效的控制^[3]。模糊控制系统的基本结构如图 3 所示。

 

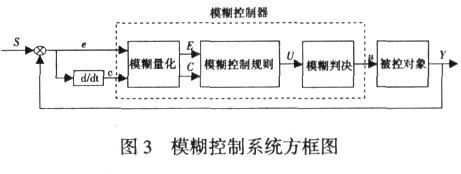
图 3 中 S——系统的设定值,是精确量;

e, c——系统偏差与偏差变化率,是精确量, 它们是模糊控制器的输入;

E, C——经模糊化处理后偏差与偏差变化率的模糊量;

U—— 模糊量的偏差与偏差变化率经模糊控制规则、近似推理处理后, 得到模糊量的控制作用;

u——模糊量的控制作用经模糊判决后得到的精确的控制作用来控制被控对象;

Y——系统的输出。

基本论域中去, 其取值由控制量 U 的模糊集和实际对象的控制量大小来决定。

( 1) 模糊量化: e、e , 分别为偏差与偏差变化率,

u 为输出, 取其基本论域为:

 

E=[- 15, +15] E =[- 10, +10] U=[- 20, +20]

将上述基本论域量化为模糊集论域:

E&X={- 6, - 5, - 4, - 3, - 2, - 1, - 0, +0, +1, +2,

+3, +4, +5, +6}

 

E &Z={- 6, - 5, - 4, - 3, - 2, - 1, 0, +1, +2,

+3, +4, +5, +6}

U&Z={- 6, - 5, - 4, - 3, - 2, - 1, 0, +1, +2

+3, +4, +5, +6}

误差 e 的量化因子 Ke=6/10=0.4;

误差变化率e 的量化因子 Kc=6/10=0.6;

控制量变化 u 的比例因子 Ku=6/20=0.3。

( 2) 确定模糊子集及隶属度表: 设 A, B, C 分别为 X, Y, Z 的模糊子集

A={PB, PM, PS, PO, NO, NS, NM, NB}

B={PB, PM, PS, O, NS, NM,  NB}

C={PB, PM, PS, O, NS, NM,  NB}

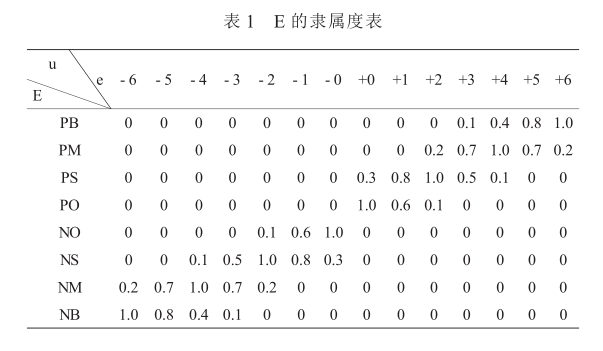
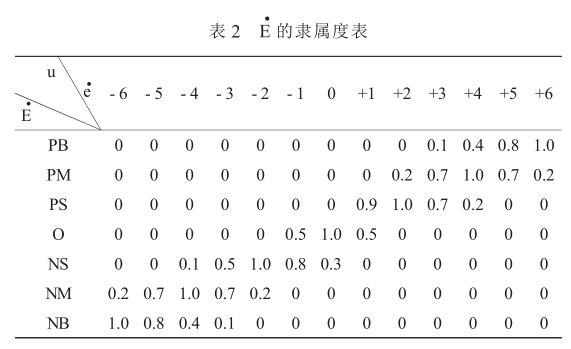
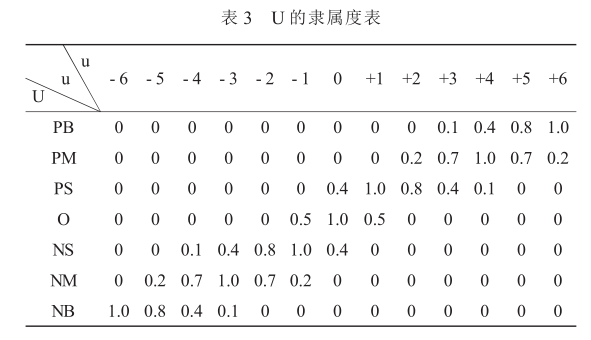
选取隶属函数为正态分布时, 对模糊子集 A, B, C 确定其量化论域中各元素的隶属度如表 1、表2、表 3 所示。

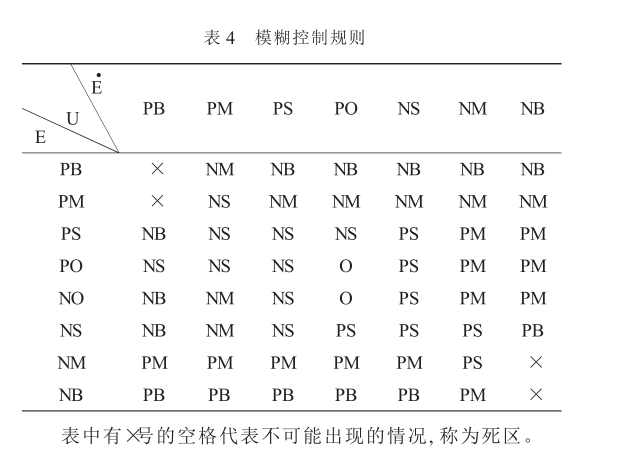
( 3) 根据振动给料机操作经验, 总结出模糊控制规则表如表 4。

(4)由于模糊集合 E 有 14 个元素, E 有 13 个元素, 因此

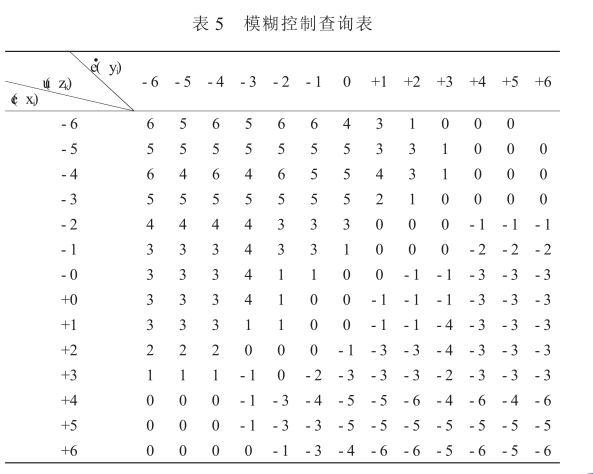
可求得输出语言变量 U 的模糊子集 Uij 有 14×13= 182 个。根据上面得到的模糊子集 Uij, 应用加权平均法对其进行模糊判决, 可以得到相应的控制量 u, 进而得到整个模糊控制查询表, 如表 5 所示。