

来源:更新时间:2020-09-29 10:44:02点击次数:4457次
1引言
皮带输送机是散装物料常用的运输设备,通常采用电子皮带秤在物料的运输过程中完成对物料的累计计量。相对于静态计量设备,电子皮带秤难以满足贸易结算、能源计量、节能减排等等较高精度的应用要求。
目前对于称重的研究重点基本集中在“皮带效应”,根据经验对某一个或某几个敏感参数进行线性补偿;或者通过对皮带的特性进行力学分析,尝试建立简化的力学模型在理论上对误差进行计算和补偿。但实际皮带秤作为为动态累计计量设备具有更高的计量效率,但同时电子皮带秤计量精度普遍不高、耐久性差,国际建议OIMLR502014(E)将皮带秤划分为0.2、0.5、1.0和2.0这4个准确度等级[2]。由于受到被称物料的流量、速率、环境以及随时间累积的皮带蠕变等因素。
电子带秤在工作时,皮带秤称重误差影响因素众多,并且呈现非线性和相互作用,所以仅用理论分析试图找出其规律、追求精细化补偿模型相当困难。也有学者将人工智能理论、机器学习等新兴技术都引入到了传统的动态称重领域,不过将机器学习应用于优化电子皮带秤的动态称重精度的研究目前较少。
本文引入过程神经网络提高皮带秤动态称重精度,增强了皮带秤的耐久性,同时给出了皮带秤的耐久性考核方法。
2过程神经网络模型参数确定
2.1过程神经网络
随着计算机技术、人工智能技术在各行各业的成熟运用,国内外越来越多的研究将神经网络这一机器学习理论引入动态称重误差建模和校正补偿[5]。神经网络利用物理器件来模拟生物神经网络的结构和功能,将多个神经元按照一定的网络拓扑结构组合起来对分布式信息实现并行处理,从而得到一个描述系统输入、输出关系的非线性映射[6]。
基于神经网络理论的运用,对影响皮带秤动态称重精度的误差源进行分析,挖掘关联性,提取参数特征,通过适当标定获取皮带秤运行过程中与称重结果可能有关的数据,再利用神经网络等机器学习方法寻求可用、可靠的经验关系,相比理论分析更具有可行性和实用性。
传统的人工神经网络都是网络输入与时间无关的模型,而皮带秤在运输过程中,称重区间的称重传感器会连续地得到称重段皮带上物料的重力信号,这个信号的连续变化贯穿物料运输的始终。因此很难找到一个合适的数据作为神经网络的输入信号。在人工神经网络的发展中,有学者提出过程神经网络的理论,并证明了理论的可行性[7]。过程神经网络是人工神经元网络在时间域上的扩展模型,其输入是与时间相关的量,输出是静态的量,这种过程式的输入、静态的输出刚好与皮带秤的输入输出形式相符合,因此过程神经网络相比传统的人工神经网络更适合用于改善皮带秤动态称重精度的研究。
2.2皮带秤工作原理
目前的皮带秤主要通过积分法来获取物料的累计重量:当输送带把物料输送到称量段上时,称重传感器和测速传感器分别测得称量段上的瞬时重量Wl(t)/kg和同时刻输送带的瞬时速度v(t)/
m·s-1,假设称量段长度为l/m,整个称重过程时长为T/s,则所输送物料的累计重量I为[8]:
I=∫TWl(t)v(t)dt
秤称重误差的重要因素,对称重结果的影响无法消除,且随着称量段物料的改变实时变化,故直接测量皮带张力难度较大。专家和学者对皮带秤张力检测方法进行过大量研究,发现垂度变化和张力变化具有强相关性,比较实用的是建立张力和垂度间的关系,通过监测称重托辊间皮带垂度变化来间接反映皮带张力变化[8,9]。垂度变化指称重过程中称重托辊中点处皮带相对于其空载时的下垂量,如图2所
示,垂度变化量Δh=hh0,其中h0为空载时皮带垂度,h为加载物料时皮带垂度。
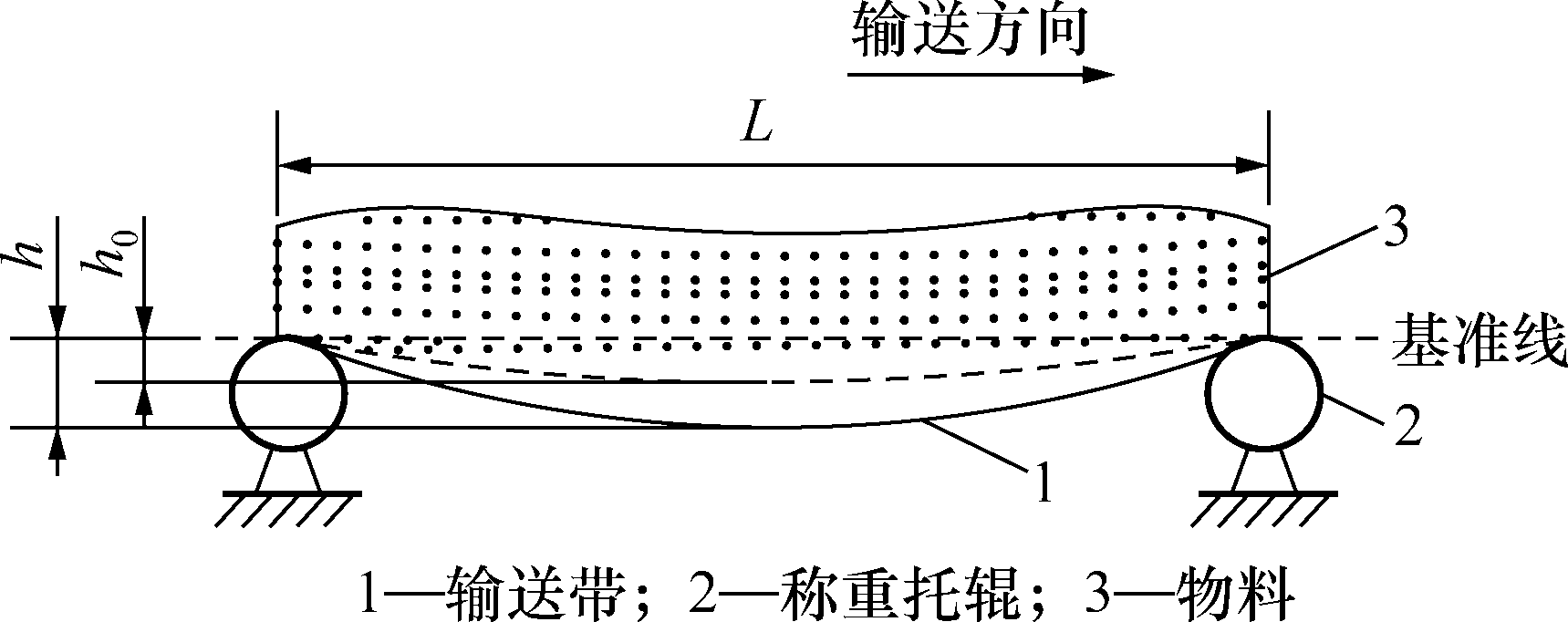
图1垂度变化示意图
Fig.1Schematicdiagramofvariationinbeltsag
结合对皮带秤称重原理分析,将单位长度上的重量、皮带速度、皮带垂度变化选为输入,将累计物料的实际重量(静态称量获得)作为输出,构建一个3输入、单输出、含有一个隐含层的过程神经网络。
3过程神经网络算法设计
过程神经网络中采用过程神经元代替传统的神经元,过程神经元由加权、聚合和激励3部分组成[9],是对传统神经元的聚合运算机制和激励方式向时间域进行扩展,使神经元同时具有时、空二维信息处理能力。单个过程神经元如图2所示。
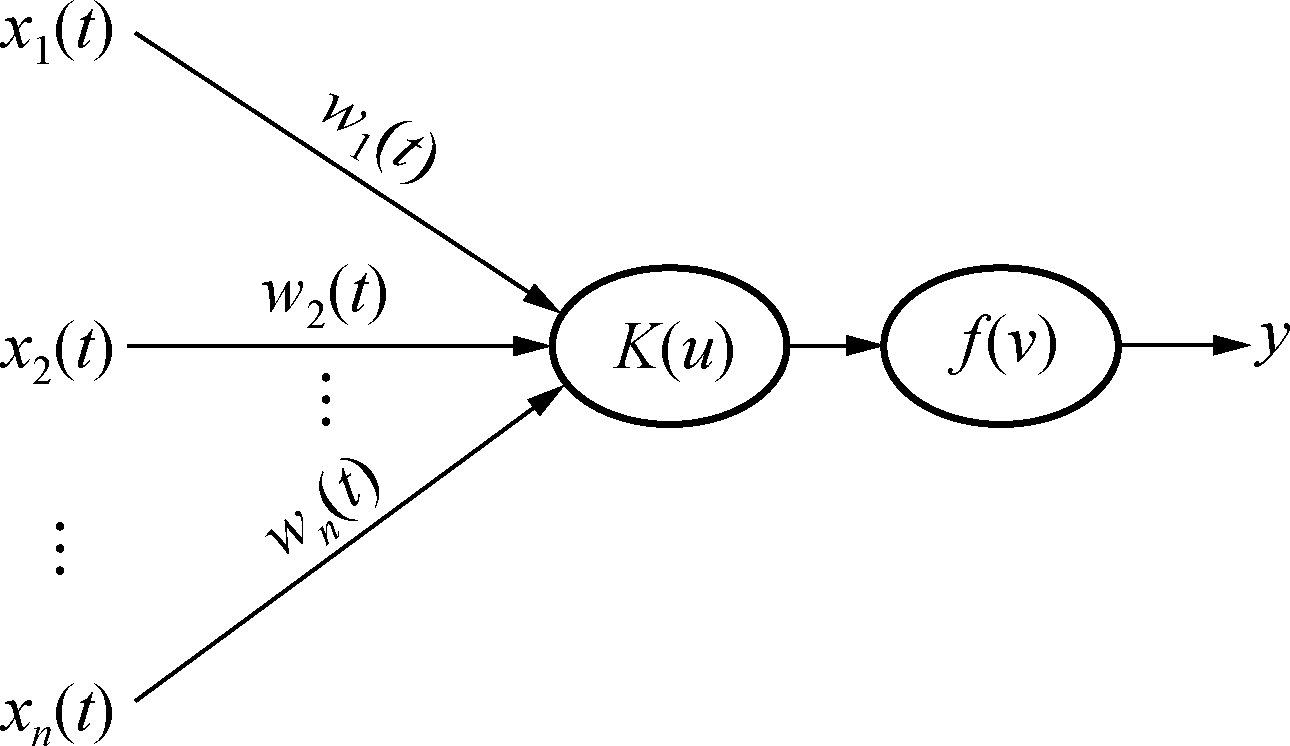
图2单个过程神经元示意图
Fig.2Schematicdiagramofsingleprocessneuron
图2中,x(t)为输入向量,w(t)为权值函数,
K(u)为时间聚合函数,f(v)为激励函数,其中输入0l
2.3模型参数确定
皮带张力是皮带秤的基本属性,又是导致皮带向量和权值函数皆是一条与时间t有关的向量序列,时间聚合函数一般为积分的形式。图2中过程神经元输出为:
y=f∫T∑n
w(t)x(t)K(t)dt-θ
(1)
x(t)=∑
xp·b(t)
式中:θ为神经元阈值;T为输入量持续时间;n为由于b(t)是正交基函数,所以有:
输入量数量。
与传统神经元不同之处在于过程神经元的输入和权值可以是时变的,其聚合运算既有对空间的多
∫Tbl(t)·bp(t)dt=
则网络输出改写为[14]:
1l=p
0l≠p
输入汇聚,亦有对时间过程的累积。
nmL
y=g∑ωkjf∑∑w(jil)·x(il)
-
θj
-
b
与传统人工神经网络相同,由若干个过程神经
元按一定的拓扑结构组成的网络称为过程神经元网
j=1
i=1
l=1
(3)
络。一个多输入单隐层单输出神经网络的拓扑结构如图3所示。
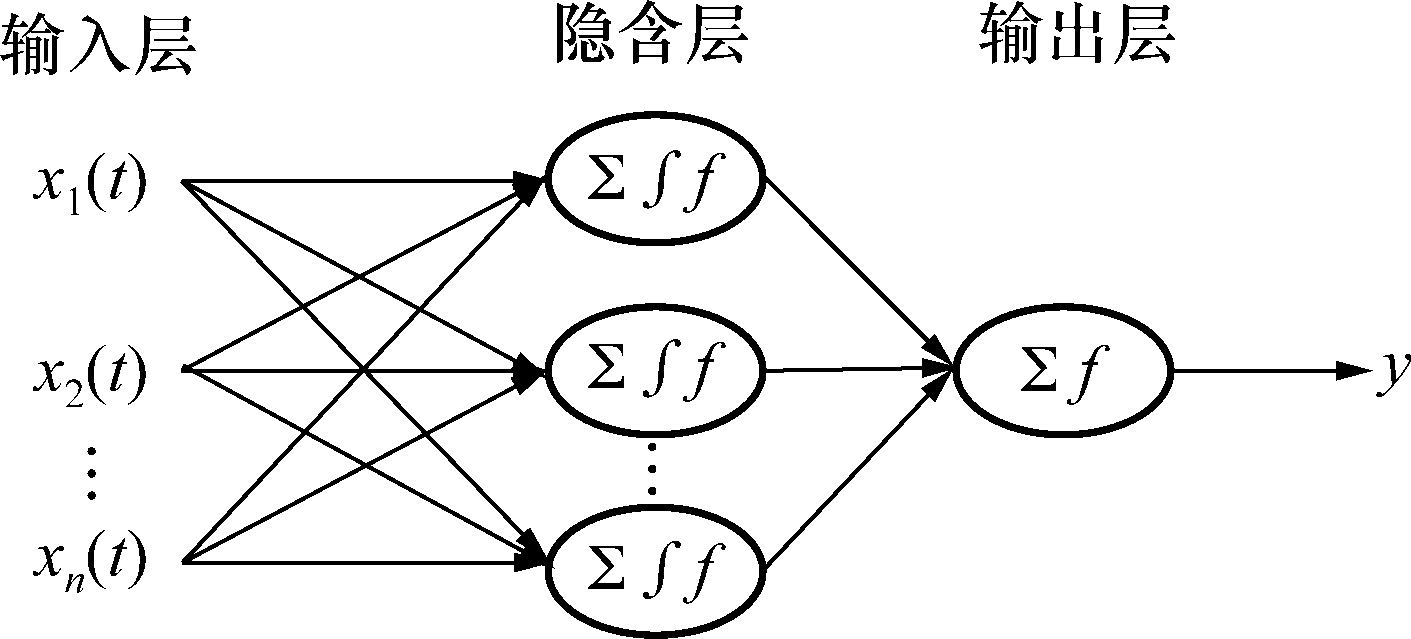
图3神经网络的拓扑结构图
Fig.3Topologyofneuralnetworks
若以m个输入层神经元,n个隐含层神经元,1个输出层神经元为例,则过程神经网络的输入输出关系为:
由式(3)中可见,经过在正交基底下展开的过程,将积分的运算转化为m×L项相加,因此简化了积分过程的运算,只要调整隐含层神经元数量m和权值基函数数量L就能改变积分运算的复杂程度,摸索合适的网络模型规模就更为方便了。
基于前人的研究经验,本研究将输入函数和权
值函数通过FFT(快速傅里叶变换)在三角函数基底下等精度展开,得到式(3)所述的输入输出关系。网络权值更新方法基于已广泛使用的BP神经
网络算法的梯度下降法[15,16]。
给定K个学习样本,设输出真值为dk,则网络训练误差为:
E=1K2
y=g∑j=1wkj·
则有:
2∑k=1(ykdk)
f∑∫T∑L
w(l)b(t)x(t)dt-θ-b
(2)
w(jil)
=w(jil)
+ηΔw(jil)
i=10
l=1jilij
式中η为学习速率。
式中:g()为线性函数;f()为sigmoid函数;k为输出
Δw=-E=-
(yd)·f(u)
层神经元;bl(t)为权值基函数,即将权值函数w(t)改写为以权值基函数为基底展开的形式;L为基值
kj
其中:E为误差;
wkj
∑k=1kk
函数数量;b为输出层阈值。mL
u=∑∑ω(jil)·x(il)θj;
过程神经网络与传统神经网络相比,有一个额
外的积分过程,但由于输入信号为离散采样的数据序列,并不是已知解析表达式的连续信号,所以积分
只能通过数值计算实现。实际应用中,当采样率较
i=1l=1
Δw(jil)=-E
ji
Δθ=-E=
=-(ykdk)·ω·kjf′(u)·x(il);
k=1
(yd)·w·f′(u)。
高时,样本的数据量极为庞大(上10万个数据点),
jθj
∑k=1kkkj
这种情形下,如果采用直接累加的方式计算积分,不仅计算量庞大,耗时较长,而且由于系统的输入是由
具体问题确定的,权函数的形式具有任意性,因此在训练中存在不稳定性,且计算复杂度高[10]。
为了解决这一问题,有学者发现,将输入函数和权值函数在同一正交基底下等精度展开,能够避免冗余的叠加,还会使网络的学习速度明显加快[11]:
将权值函数和输入函数在同一个正交基底下展
开得[12,13]:
由于f(u)为sigmoid函数,所以有:
f′(u)=f(u)·(1-f(u))算法描述如下:
Step1:给定误差精度e;累计学习迭代次数q=0;学习最大迭代次数M;选取权值基函数b(t)个数L,l=1,2,3,…,L。
Step2:初始化权值和阈值。
Step3:计算误差函数E,如果E<e或q>M转
Step5。
wlStep4:修正权值和阈值;q+1→q;转Step3。
ji(t)=∑l=1wji·bl(t)
Step5:输出学习结果,结束。
4算法仿真验证
次学习之后误差下降速度逐渐放缓,直到第100次学习时误差已降到0.1,又经过了49次学习将网络误差优化到网络学习误差精度要求。
在实验室里搭建实验系统,进行数据采集实验共获得18组数据,每组数据包含可能影响皮带秤称重精度的3个关键因素:单位长度上的重量、皮带速度、皮带垂度变化,采样速率为2000Hz,平均每组数据有50万个点位,18组数据中,前14组加上空载运行数据组成共15组数据作为训练组,后4组数据作为测试组。
将单位长度上的重量、皮带速度、皮带垂度变化作为3个输入层神经元的输入,选取隐含层神经元数目为5个,权值基函数数目为128个,网络误差精度0.001,仿真程序在matlab环境下编写和调试。读取数据后,对数据进行预处理:截取称重时段内的数据以减少总体数据量;根据一定的算法通过速度信号(信号为周期性脉冲形式)计算皮带速度;将重量信号、速度信号、垂度变化信号进行给定精度下的FFT(快速傅里叶变换)处理。
由式(3)可知,将权值函数和输入函数在正交基底下展开后,网络输出关系式中可以看到,输入层到隐含层的权值数量为m×n×L,因此在matlab中定义三维矩阵用以存储输入层到隐含层的权值,定义二维矩阵储存隐含层到输入层的权值和隐含层的阈值,实际研究中发现输出层阈值对网络收敛性影响过大,固未使用输出层阈值b。首先遵循BP神经网络的方法将权值阈值初始化,初始化结果为将训练组输入数据代入训练完成后的模型,所得模型输出与训练组实际输出数据对比如图5所示。
由图5可以看出训练完成后的模型拟合效果较好,网络输出与实际输出几乎一致。
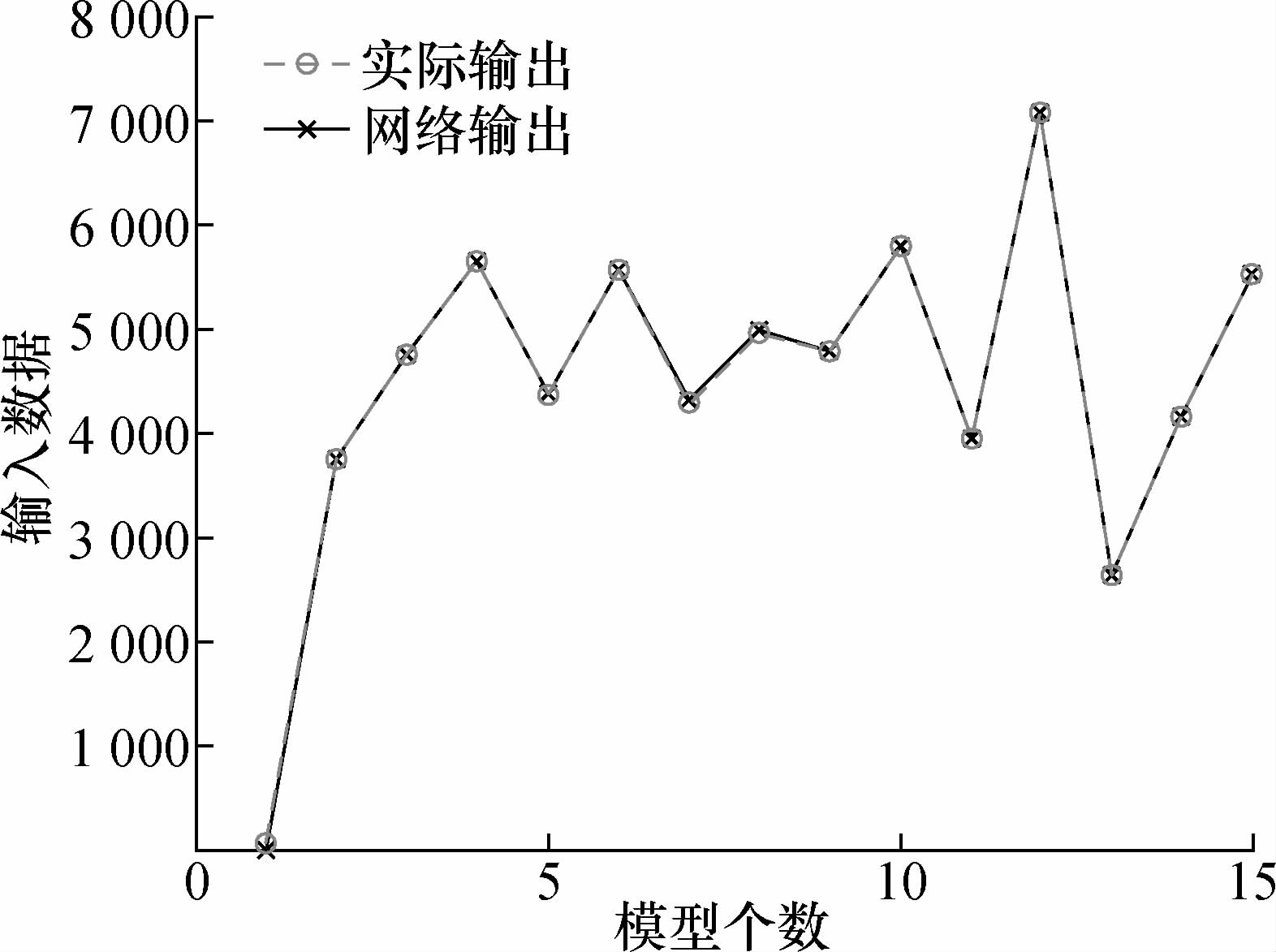
图5网络输出与实际输出对比
Fig.5Contrastbetweennetworkoutputandactualoutput
将测试组输入模型后,测试组误差达到1%。得到利用过程神经网络模型对皮带秤动态称重误差补偿前后的结果对比。
(-1,1)区间内的随机数,然后对FFT处理后的输入数据和输出数据做归一化处理并代入网络进行训练。网络学习误差曲线如图4所示。
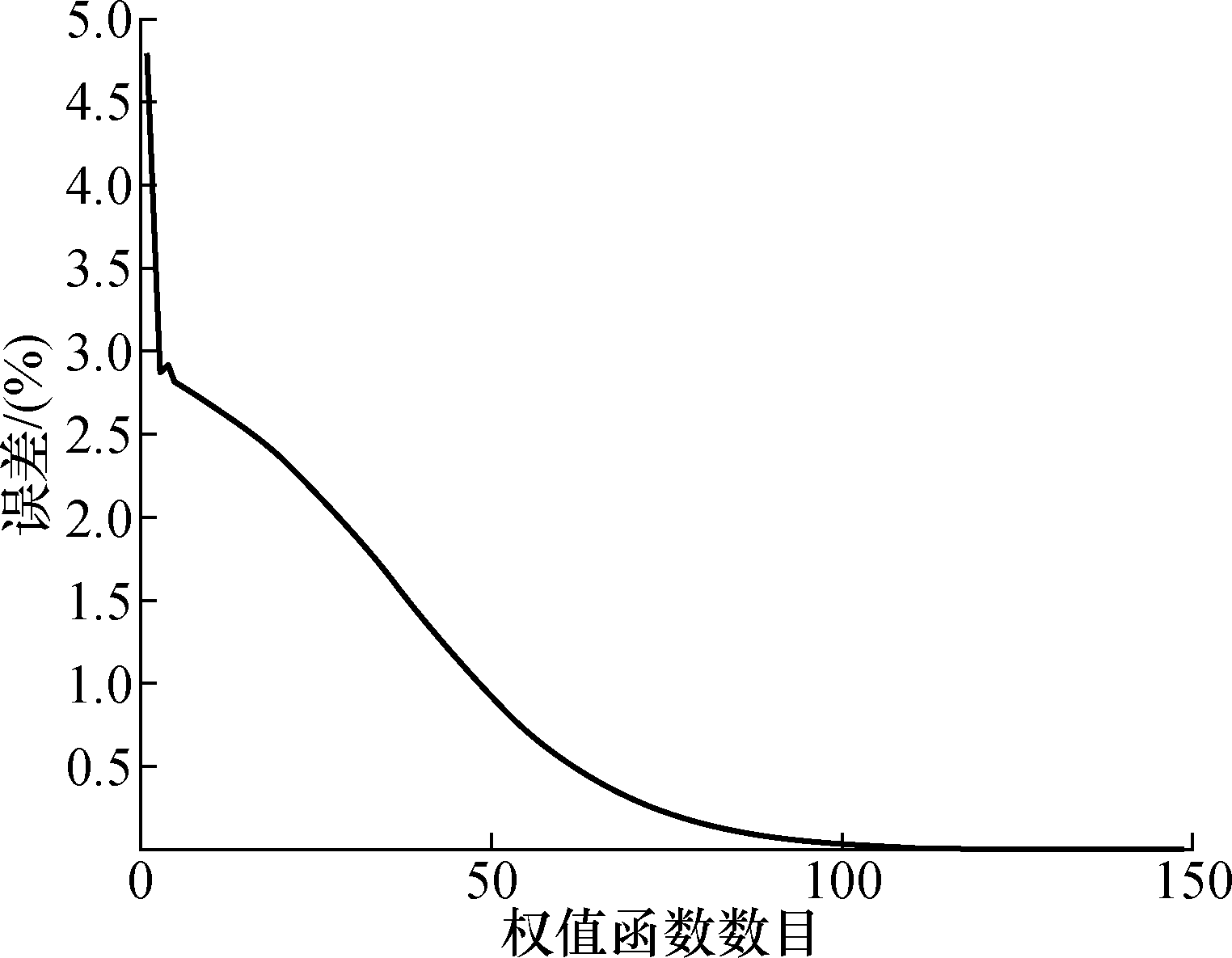
图4学习误差曲线图
Fig.4Curveoflearningerror
模型经过149次学习优化达到网络精度要求,由于采用了梯度下降法作为参数更新规则,所以前100次学习中,网络误差在学习初期快速下降,第1015643.05703.55656.51.070.2425791.05875.05792.21.450.0234350.04299.54305.6-1.16-1.0247069.67142.57081.61.030.17
由表1中结果可知,4组测试组中,使用网络模型补偿后新误差均较使用网络前的原误差有所降低。除了第3组误差降低不明显外,其余3组误差皆降低显著,明显优于使用过程神经网络算法前的误差,说明文中所建过程神经网络模型是可行有效的,可明显提高皮带秤动态称重精度。
5结论与展望
将过程神经网络引入皮带秤的动态称重精度补偿研究中,算法推导正确无误,模型拟合较好,通过测试验证了模型的可行性和有效性。由于采用梯度下降的权值更新方法,极少情况会出现网络学习误差陷入局部极小值导致达不到目标训练误差。但由于前期训练和测试样本数量较少,且模型选取的基函数数量、隐含层神经元数量与模型训练速度、收敛效果之间的经验关系还需进一步研究摸索,故当前模型的泛化性能仍有改善空间。此外,当前研究中采用的输入数据是数采卡直接采集,称重段数据为人工提取,称重信号在测量、提取过程中是否存在对称重结果误差的影响目前还不得而知,称重信号是否存在失真,噪声对称重误差的影响也还需要相关深入的研究。
文章来源于网络转载,侵删
 ×
×