颗粒包装秤是针对颗粒状、流动性较好的物料设计而成的包装秤，具有称量精度高，操作简单方便、可靠性强等特点，广泛应用于饲料、粮食、食品、种子、精细化工等行业。衡量一台包装秤效果的技术指标主要是测量精度和定量速度，而这两者之间是相互矛盾的关系，较高的测量精度必然导致定量速度的降低，而同时提高速度和精度通常只有在硬件上进行改进⑴。例如SCHENCK扭环式称量传感器RTN0.05/330T,它的精度高且量程大，但其成本也高，不满足国内大范围的使用。随着包装机械行业的迅速发展，对定量包装技术的要求越来越高，对于大规模生产的企业来说，速度快且精度高的包装设备无疑能够减少大量成本，因此对包装秤定量速度和测量精度的研究是一项重要的课题。目前国内对包装秤的大部分研究都是关于如何提高测量精度的，对定量速度的研究文献较少。
定量速度是指包装秤称量单位质量物料所用时间的长短，一般单位为包（袋）/min,因此减小定量所需时间即可提高定量速度，定量过程是包装全过程的主要部分，提高定量速度就意味着提高包装速度。这里选取DB8320型立式颗粒包装秤作为实验对象⑷，主要通过实验和数学算法优化给料方式，达到缩短定量周期的目的，从而提高包装秤定量速度。
1包装秤结构及工作原理
1.1结构组成
定量包装秤的结构组成包括储料仓、给料装置、称量控制系统、卸料夹袋及其他相关辅助机构，各机构相互配合，按照要求完成整个包装过程。影响定量速度和测量精度的关键部件是称量控制系统，它包括了称量斗、承重支架、称量传感器、PLC、触摸屏、电机等；给料装置与气动控制的截料门配合下料仓动作，实现分级给料；卸料夹袋机构同样由气动控制，配合控制单元的反馈信号按照预设程序进行操作。某定量包装秤结构见图1。

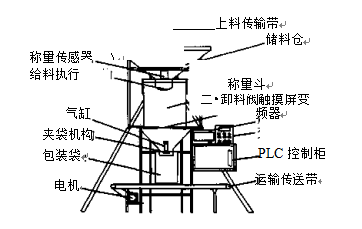
图1某定量包装秤结构
Fig.lStructurediagramofaquantitativepackingscale
1.2工作原理
先将包装袋套于卸料斗上并由夹袋机构夹紧,当进入工作状态后，由变频器控制上料传输带开始下料，控制系统打开给料执行机构，该给料装置通过气动控制截料门位置改变下料口尺寸从而实现粗、精两级给料；称量传感器将采集到的质量模拟信号转变为数字信号输入控制系统；当检测到称量数值达到预设值时，控制系统将信号反馈至给料执行机构、卸料阀和夹袋机构并及时动作，当称量达到最终设定值后包装袋落到传输带上运至下一个工位，一个周期结束，自动开始下一袋的包装。
2影响定量速度的因素
2.1给料量与称量时间
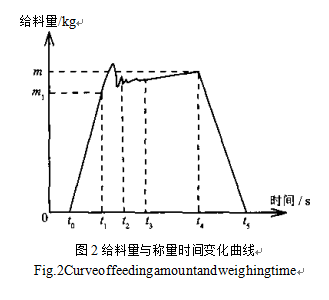
根据给料量和工作时间的关系及定量包装秤的工作原理可以绘制出称量曲线，见图2”—也0-而表示下一包装周期稳定、回零时间；而-fi表示粗给料时间；在前一级给料即将结束时称量值会瞬间变大，根据冲量公式Ft=mvY-mv2可知，vi和v?差值越大，尸越大，这一过程称为过冲现象，为避开过冲现象时出现的虚假波峰值应设置t,-t2冲量禁止判别时间（用tf表示），且禁止判别时间不能过长，一般取0.3-0.5之间If表示波峰值回落后称量斗还会持续轻微震荡一段时间，此时称量仍处于不稳定动态称量状态（用f表示）；存-4表示震荡过程结束，开始以V2稳定精给料速度给料，此时称量状态趋向于静态称量（用4表示）；金-，5表示待称量达到设定的目标称量值后立即打开卸料门开始卸料。由于包装秤稳定回零时间、禁止判别时间以及卸料时间基本是固定的，所以文中主要从优化给料速度和粗、精给料切换方式的角度来分析如何缩短定量周期，即图2中姑-4阶段。

2.2给料速度
给料口单位时间内通过的给料量称为给料速度，给料速度越快则定量时间越短、误差越大，但要保证误差在精度要求范围内就必须使精给料速度很小，而给料口的通过能力对给料速度有着很大的影响，具体可由下面的公式计算3。
对矩形给料口：
对圆形给料口：
式中：m为给料口的通过能力；为物料的堆密度；g为重力加速度；7p为物料的形状系数，对于球形颗粒,而=1.6；对于非球形颗粒,fp~2.4；d为颗粒直径；兀为角度系数tan伊"为料斗中心线与料斗壁的夹角，当£<45。时，戶按料斗休止角计算；当戶>45。时，无=1.0；，和3表示矩形出料口的长度、宽度；Do表示圆形出料口的直径。
给料速度可通过调节给料口尺寸大小来改变，这里选用的包装秤采用的是气动执行机构，优点在于执行速度快，使用较方便，并且可以通过调节截料门位置改变给料口下料尺寸来实现不同速度给料
2.3粗、精给料切换方式
一般的两级给料机构为当粗给料达到设定值的90%左右时，切换为精给料继续完成剩下10%的给料。粗给料量越接近设定值，总定量时间越短，若要求测量精度高，则应保证精给料时间。确定最佳给料切换方式就是确保精度的最小精给料量。在实际工作过程中，有以下几个方面对精给料过程造成影响。
1)过冲现象对测量结果会造成较大影响，目前主要有2种改善方法:设置冲量禁止判别时间Zf,以避开瞬间虚假波峰值；采用增加一级给料的方式，减小前一级的给料速度从而降低过冲的影响卩方，但这种方法使得称量结构复杂、成本增加且不易把握最佳切换时间。
2)粗给料切换到精给料需要足够长的稳定时间f才能保证测量精度不受称量斗震荡的影响，且前一级粗给料速度V1越大，对称量斗造成的震荡影响也越大，所需稳定给料时间越长卩气这两者之间存在一定的变量关系，通过实验方法可找出这一关系式。
3)粗给料过程会产生定量误差△皿，为避免岀现由于误差叠加导致精给料过程未结束就已经达到称量目标值，精给料量必须要大于粗给料误差值A皿，保证误差值稳定前精给料过程还在继续卩可。最小精给料量必须大于或等于这三者之和，即m2>\mx+v2(Zf+rp+Zq),V2为精给料速度。
3实验
3.1材料
丝苗米(长粒形釉稻优质稻米，米粒型宽长比22:8,长度5.4~6.6mm,千粒质量<12.59g)A计时器、计算器、合肥中联DB8320型立式包装秤，通过液晶触摸屏监控并显示实时质量，称量系统通过使用JLBS-P铝合金S型称量传感器(量程0~10V)输出质量信号，采用16位BSQ-2变送器，整个系统稳定可靠，包装效果良好。
3.2方法
根据上文的分析，要得出给料速度v和定量误差的关系和精给料速度与动态震荡时间0+4)的关系，分3个步骤:调节给料口落料尺寸分为1~10档，分别测量每一档称量10kg丝苗米所用的时间和实际质量，为提高准确性，每档分别测5组后取平均值，将实际质量除以称量时间即为此时的给料速度，而实际质量会大于10kg是因为在给料截止后称量斗中还有部分空中料柱处于下落状态，测量数据见表1;对以上10组测量数据可用Matlab
表1称量10kg丝苗米实验测量数据

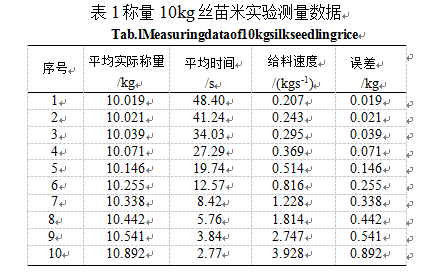
软件计算关于给料速度和误差的n次多项式回归方程[16~17],根据所求关系式求出保证精度要求的最大精给料速度％；调节粗给料速度V1(较大)进行称量，记录从VI切换到V2所需要的动态震荡时间(tfHq)并得出回归方程，由公式计算出最佳给料方式的相关参数，对包装秤设定该参数进行试验验证，将不同给料方式下测得的定量周期进行对比分析。
4结果与分析
4.1给料速度与定量误差的曲线关系
根据表1数据，可以在Matlab中调用polyfit函数对给料速度和定量误差进行拟合，它的基本调用格式为P=ployfit(x,y,n),表示用n次多项式拟合数据点笛，如其中X为给料速度，V为误差。在Matlab命令窗口输入以下命令:
»x=[0.2070.2430.2950.3690.5140.8161.2281.8142.7473.928];
»y=[0.0190.0210.0390.0710.1460.2550.3380.4420.5410.892];
»P=polyfit(x,y,3)
输出结果为：
P=0.0380-0.23990.6114-0.1126
n的值分别取了2〜6次，对比每种函数形式的拟合程度，得出"取3次时拟合程度最好，因此给料速度和定量误差拟合的回归方程为△〃=0.038v3-0.2399V2+0.6114v-0.1126,回归曲线见图3。
验规则卩叫称量10kg物料的精度要求在0.3%以内。计算出当要求精度为Am=0.03kg时，最大精给料速度v2为0.258kg/s,且此时测定保证精度最小静态稳定称量时间4=0.8So调节给料速度进行多次实验，记录从巧切换到樨所需要的动态震荡时间，厂上，见表2,其中4为平均时间。

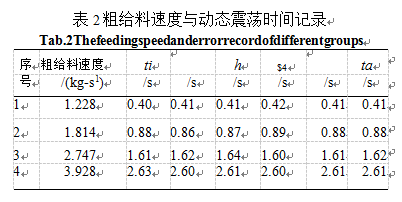
利用Matlab软件对粗给料速度和动态震荡时间进行拟合，再次调用polyfit函数，a表示粗给料速度，b表示动态震荡时间，因为从散点图来看离散点分布几乎趋向于一条直线，因此〃在这里取1次，在Matlab命令窗口输入以下命令：
»a=[1.2281.8142.7473.928];
»b=[0.410.881.622.61];
»P=polyfit(a,b,l)
输出结果为：
P=0.8138-0.5969
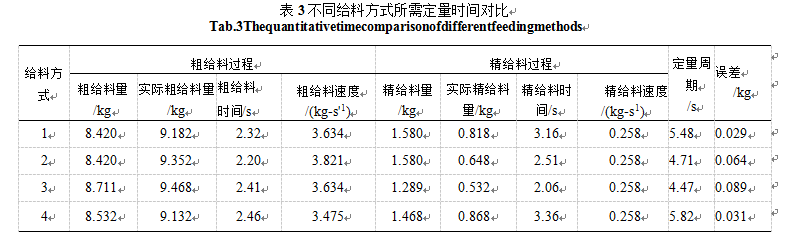
可以得到拟合的回归方程为时上=0.8138巧-0.5969,回归曲线见图4。

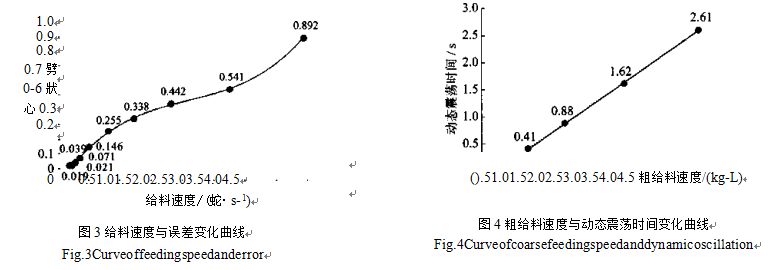
4.2粗给料速度与动态震荡时间变化曲线
从给料速度与误差变化曲线分析，给料速度与误差呈正相关关系，且当给料速度小到一定程度后误差变化幅度开始减小，逐渐趋向于0.02kg左右。根据JJF1070—2005定量包装商品净含量计量检
4.3最佳给料方式计算
根据上文分析，理论上包装秤的定量周期计算式为：

式中：vi,V2为粗、精给料速度；代，t2为粗、精给料时间；4为冲量禁止判别时间；上为避开虚假波峰值后持续的动态震荡时间；fq为保证精度要求的最小静态稳定称量时间；△皿为粗给料速度V!对应的误差，m为目标称量值，m2,如，分别为预设精给料量和实际精给料量；T为定量周期，且应使『的值最小。代入数据得：T=四丝-0.038%2+1.0537%-0.6183
这样就得到关于定量周期和粗给料速度的方程，显然只要求出最小周期T对应的粗给料速度vi即可。接下来用Matlab解析法和图解法求解函数极值[19-20],调用ezplot()函数，在Matlab命令窗口输入以下命令：
»symsv;f=-0.038*vA2+1.0537*v-1.4183+10.267*vA(-l);
»fl=diff(f,v);
»ezplot(fl,[0,4])
»v0=solve(fl),ezplot(f5[0,4])
»eval(vO)
ans=
3.6338
»f2=diff(fl);b=subs(f2,v,v0)
»eval(b)
ans=
0.3519
»v=3.6338;-0.038*vA2+1.0537*v-0.6183+10.267*vA(-l)
ans=
5.5343
»v=3.6338;0.038*vA3-0.2399*vA2+0.6114*v-0.1126
ans=
0.7647
由程序生成的定量周期一阶导函数曲线和定量周期函数曲线见图5—6。计算可得，当vi=3.634kg/s时，定量误差值△皿=0.765kg,最小定量周期7=5.53s,粗给料时间n=2.32s,预设粗加料量wi=8.42kg,实际粗加料量wi'=»?i+A»2i=9.185kg,精给料时间t2=t”p+妒3.16s,实际精给料量0.815kg。

4.4试验验证
为验证上述算法得出的最佳给料方式的有效性，对包装秤称量控制系统设置了4组不同给料方式进行称量实验并记录数据，见表30方式1应用了上文计算的最佳给料切换方式；方式2釆用了与方式1相同的粗、精给料量，不同的粗、精给料速度；方式3采用了与方式1相同的粗、精给料速度，不同的粗、精给料量；方式4采用了与方式1不同的粗、精给料量，不同的粗、精给料速度，但保证测量精度。实际测量数据与理论计算数据存在小范围的偏差，但基本一致，不影响验证分析。
从给料方式2和方式3的测量结果可以看出，虽然提高粗给料速度或增加粗给料量可以较明显地缩短定量时间，但是无法保证测量精度在要求的0.03kg以内，误差分别达到了0.064和0.089kg,这2种情况下称量都没有满足最小精给料量,方式4降低了粗给料速度和粗给料量，虽然精度基本达到了要求，但定量周期相比方式1增加了0.34S。

5结语
文中分析了影响颗粒包装秤定量速度的主要因素，提出了通过优化给料速度和粗、精给料切换方式来缩短定量周期，从而提高定量速度；给料速度与误差及动态震荡时间之间存在一定的关系，且实验中发现粗给料速度与动态震荡时间几乎成线性关系，可运用Matlab软件拟合出关于2个变量的回归方程；给出了最小精给料量和定量周期的理论计算公式，并详述了运用Matlab软件求解最佳给料方式相关参数的方法。从实验结果表明，利用上述最佳给料方式进行定量包装确实可在保证精度的要求下缩短定量周期。该方法还可应用于其它同类型的包装秤，便于提高工作效率。

文章来源于网络转载，侵删