1问题的提出
颗粒型全自动包装机的物料供应装置是一个转盘式定量供雌。对于颗粒、飾和片剂物料，主要采用量杯式定容计量E0定量供料器为转盘式结构，从料桶流入的物料用沿圆周均布于转盘t的若干个(T^4个關或6个)量杯进行连续定容计量，然后，物料由于自重而自动充填入包装袋内,配合制袋进行装填包装⑶。帯朧置和供料系统的有机完美配合才能包装好一袋袋电的产品。睡的大小18决定着歹效率的高低。转盘转得慢，单位时间内生产的产品袋数就少，但是，量杯内的物料可骥全地8H成騰充期球§内。踊，如果聞蔑H高,超过了一定限度，物料还未来得及落进成形器口，就被旋转的量杯带走了。这样Ft造成了计量的不准确，致使每袋的物料比预装量少了一些。为了解决这一问题,使量杯内的物料全部一粒不留地落进成形器,保证每袋产品的净含量达到预定值，下面以力学学为理对行分析计算,从而得到准确的公式。

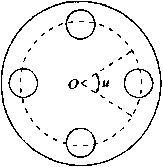
图1计量转盘和量杯

Fig.1Measurementtumplateandmeasuringcup
2分析计算的前提条件
为了便于分析落料过程的实质，特作以下几点假设和简化:颗粒都看作是理想的散粒体3」；颗粒的下落流动理解为理想状态下的运动;颗粒的大小相等且质量都为m(kg)；颗粒与量杯相比足够的小;忽略颗粒间的摩擦力和空气的阻力。为了不失一般性，特作以下几点设定:假设量杯都为截面圆直径为5(m)，深度为H(m)的空圆柱体;假设转盘的转速为n(r/s);成形器口的2个侧边对应转盘的圆心角为0(rad)，见图1。
3基于力学的分析
随着量杯底面活门的打开，量杯中的物料相继落下。容易知道，最可能留到量杯里的物料必定位于量杯最上层，见图2左上图，且位于旋转方向上的后侧，见图2左下图。在这些颗粒中(以颗粒q、c为例，见图2右图),b、c由于受力在任一瞬时的

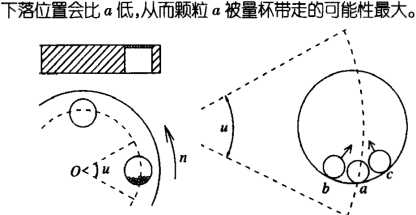
图2量杯中物料的下落

Fig.2Pelletsfallingdownfrommeasuringcup

=0/(2tt    (9)
上式中,g为定值，可取9.82决；成形器和定量转盘一旦给定，。和反即是定值。
由此可见，要使颗粒全部落下,转盘的转速不应超过其极限值n解=0/(2”顽有)。也就是说，在转盘的转速不超过％陨的情况下，量杯计量相对精确，逬入每个包装袋内的物料为预定值。
5验证
现在考察颗粒a的受力情况。它受重力G和量杯对它的推力F。即它受到的合力(見图3)为：
P=G+F    G=mg
其中为颗粒a的质量,kg；g为重力加速度,m/s?。

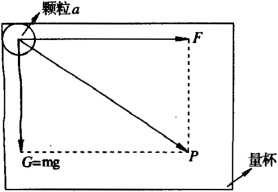
图3颗粒a的受力
Fig.3Forcesonpelleta

4基于运动学的考察
以力学为基础，现考察颗粒。在重力G和推力F作用下的运动过程⑷。
在水平方向上。=应1    (1)
即:-3/0)    (2)
在竖直方向上〃=    (3)
即：与=/2日/g    (4)
以上四式中，
e为成形器口的2个側边对应转盘的圆心角，血w为转盘的角速度，md/s；H为量杯的深度,m；勺为颗粒经过成形器口的2个側边所用的时间,s；，2为颗粒从幵始下落到离幵量杯底面所用的时间,s。
具备颗粒落入成形器的条件为：
弓＞t2    (5)
由(2)和(4)式得：    
    (6)
切yg    
即:g。/顽7?    ⑺
根据切=2”几，    ⑻
从而,转盘的极限辑度为:

对于该极限转速公式，作者在DXD系列颗粒包装机上逬行了验证，具体做法是测量了2杯的高H和成形器口的2个侧边对应賴盘的圆心角0,对公式逬行了赋值，用萝卜种子进行试验，当计量轴转速较低时,种子顺利下落，而不会被量杯带走;当把计量轴的转速渦到超过这一赋值时,发现卸料后的量杯中还剩几粒种子。经多次试验发现，转速调得越高剩余的种子颗粒数目越多。接下来，作者又把萝卜种子换成了白砂糖颗粒,发现以上的规律依然存在。这也说明，在一定条件下极限转速与颗粒种类的改变无关，公式具有普遍适用性。这就基本证明了该极限转速公式的正确性。
6结语
综上所述，可得到以下3点结论:
(1)转盘转速过高，物料容易被量杯带走,造成计量的不精确。

(2)在实际生产过程中，应控制转盘的转速，使之不超过口极限=0/(2"/g)(r/s)。

(3)不同颗粒机的极限转速是不同的,极限转速的大小取决于颗粒机本身，所以，在设计颗粒机的过程中，要对颗粒机的尺寸(这里主要是H和0)和计量精度做统筹考虑因素。
 

文章来源于网络转载，侵删