

来源:网络转载更新时间:2020-06-28 09:15:27点击次数:2837次
固定凸轮连杆组合机构在食品、纺织等机械中得到了广泛循环中应满足的应用,它的运动具有较高的精确性,能适应各种设计条件的限 制,结构紧凑,可以实现连杆机构无法实现的精确停歇的运动规 律,又能避免由于凸轮较大,传动时因偏心而引起过大的惯性 力,并能满足凸轮机构压力角和连杆机构传动角在许可范围的 要求,因此充分发挥了凸轮和连杆两个基本机构的优点,取长补 短达到较为理想的效果。这里就某厂食品包装机中的控制机械表1输入曲柄和输岀摆杆的对应关系
|
次序 |
曲柄转角" |
摆杆摆角! |
|
I |
0°f42° |
以正弦加速度向左摆动68° |
|
II |
142°t179° |
停歇 |
|
III |
179°—309° |
以正弦加速度向右摆回68° |
|
IV |
309°—360° |
停歇 |
其中"11 R 142°, "12 R 179 — 142 R 37°, 印 二 309 — 179 二 130。,
手运动的固定凸轮连杆组合机构为例进行运动分析,并作优化"14 =360 -309 =51°,女=42。,# =68。
设计
图1为这种机构的示意图。原动件1由电机通过传动系统 而驱动,2是曲柄,3是连杆,4是摆杆(输岀构件),槽凸轮和机 架相连。A、E为固定铰链,B、C、D为活动铰链,摆杆4和机械手 连成一体,它按照给定的运动规律作摆动。这种机构的运动参 数选择具有较大的灵活性,可根据结构和安装条件先确定某些 参数,然后根据运动规律来确定其他参数,也可以选择机构的某 些动力性能如机构的最佳传动角和凸轮的较好的压力角作为目 标来进行优化设计[1]。
四个阶段的摆杆运动方程分别为(推导略)
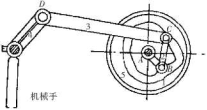
图1机构的示意图
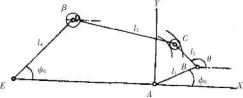
图2机构运动简图
图2为机构运动简图。按照工厂要求机架长度<5 = 522mm,输入曲柄 < =140mm,输岀摆杆长度<4 = 148mm,初始 角!0=42°,摆动行程角# = 68o,由包装工作要求确定的运动 规律,即输入曲柄和输岀摆杆对应的关系(!—")在一个运动申=地=虹[1_cos(W )]
d" "11 "11
! = !u = !0 + # =42° + 68°=110° 虫=业=0
d"
"-179° 1 . " - 179°,
!= 出3 = 出2 — # [ 7;-sin
1运动参数的计算
由图2可知,假定确定曲柄的起始位置例,则铰链B和D 的位置为
X# = Zicos( ! + !#)
Yb $ %isin( ! + !#) (5)
Xd $ %4C0S ( " + "#) — %5
Yd = %4sin( " + "#) (6)
令X= Xd - X#,Y= Yd - Yb,则铰链B和D之间距离为:
|BD| = (7)
当曲柄AB转动一周时,必定可以找到它的两个位置分别 存在丨BDI +做和IBDI血,即
当(! + ) 1 ( ! + ) mas 时,Smas — I BD I mas = %3 + %2 (8)
(! + 例)1 ( ! + 例)min 时 9 Smin — I BD I min — %3 - %2 (9)
由此可得 %3 — ( Smas+ Smin)/2
%2— ( Smas— Smin)/2 (10)
从上面式子可知,只要确定例就可求得相应的一组%3和%2。
2动力性能的验算
2. 1确定凸轮的压力角#2
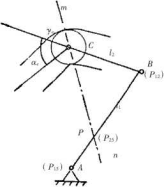
凸轮机构的压力角为销轴上受力方向和速度方向的夹角 (图3),按动力设计要求[2]应使#masV [ #> = #] -40。〜50。 取45。
为方便计算考虑#的余角,即传动角$2来进行分析$2 = 90。- #2,因此最小传动角$2 min W45?
由图2可知:
Xc = %1C0'( ! + !#) + Leos %
=%4 cos ( " + "#) + %3C0S & - %5 (11)
K = %1 sin( ! + !#) + %2sin% = "sin ( " + "#) + %3sin& (12) 由上述几式可导岀
=Xd - X# = %2cos % 一 %3cos &
Y = Yd - Y# = %2sin % 一 %3sin& 平方相加消去&可得
令 3 = X + 賢泰"営贝U 有 Xeos % & Ysin % = 3 令4 $ 贝U sin % 1 12882 cos % 1 1 +82
由(13)、(14)可得 & 1sin-i (17)
将(11) >(12)式对时间求导可得
'%2sin % - ' %3sin & = '4 %4sin( " + "#) — ' %isin( + 甲)(18) Cl%2cos% - '3 Lcos& = '4%4cos( " + "#) — '1 %1cos(甲# + !)(19) 由此解得
(O. . .
—14 sin(材+ 夕0 sin(©0 +甲_
竺= (20)
必 r ^2 sinffi-fl)
由图3用余弦定理可推得
曷队冲屈*;,;其中兀=底頒(21) 根据Kennedy定理,曲柄1,小连杆2和机架5的三个瞬心 9l(相对),9技(绝对),9l5(绝对)分别在B、A及凸轮轮廓线的 公线法+/和AB的交点9上。
(22sin $2 1 sin + AB:再广I可又 区I = J|阀2 -2厶岡COSZJgC
, 网sin乙纽C
可得 yc - sin 1 _ 一 _
J冏 +房-2厶网cos&AC
2. 2确定连杆机构D点的传动角$d
设大连杆3与摆杆4之间夹角为例,则伽=& - 180?- ("+ "0)
当例590。,传动角$D = (D (24)
例〉90。,传动角 $d = 180? - (d (25)
2.3优化过程
上式的动力要求必须满足,艮卩
$2min 6 [ $ ]
$Dmin 6 [ $ ]
釆用优化方法来进行效验:
目标函数的建立:当原动件转角(例+ !)在整个一周运动 循环中,$2min和$Dmin 之值互有关联但数值是不同的,考虑到高 副接触比低副应力大,磨损也快,故对$2作加权处理,即将 [$Dmin + 2 $2min] 1 [ $Dmin + 2 $2min ] mas 作为目标函数,由于 $2min 和 $Dmin均是原动件转角!的函数,即将求[$Dmin+2 $2min ]的极大 值变成较为简单的一维优化问题了。优化过程如下:
本文源于网络转载,如有侵权,请联系删除
 ×
×