随着衡器工业的发展以及市场的需要，定量动态称重系统得到了快速的发展，在解决称重精度和称重速度的问题上，也有了很大突破。近年来，国外比较先进的技术就有人工神经网络(ANN)技术、非线性回归(NLR)理论以及基于线性高斯法(LOG)、卡尔曼滤波(Kalmanfilter)、模糊逻辑估计(Fuzzylogicestimator)的新数字滤波器的设计⑴等。Ha-limic等人针对块状产品在传感器下的动态称重过程引入模糊逻辑估计，构成新型滤波器，借以提高动态称重速度，改善称重准确度。国内在研究定量动态称重问题上，近年来也取得了很大的进步，但是和国外的先进水平相比，还存在着比较大的差距。
笔者在目前国内外对定量动态称重系统的现有研究水平上，建立动态称重数学模型，分析误差的产生因素，提出了对关键性误差的解决方法，即加入三级下料系统和基于数字增量式的PID控制算法。
1动态称重数学模型及误差分析
称重传感器和秤体构成的称重部分可以等效为一个二阶系统⑵，如图1所示，建立称重系统的数学模型：
[M(£)+m]**+c+kx=G(t)+F(z)式中，M(z)为物料质量；G(t)为物料重量所为秤体质量；c为等效阻尼系数以为等效刚度；F(z)为物料下落的冲击力；工为秤体相对参考零点的位移。
从上式可以看出，与系统精度和速度有关的参数有,F(Z)„其中参数m,c,k与系统本身的刚体结构连接及传感器布置相关，对一个固
定系统无法改变。参数G(i),F(O在动态称重过程中会随着物料的下落而改变，模型就会随时间而变化，此系统就是一个典型的时变线性系统。因此，对于定量动态称重系统，误差的主要来源就在于参数G(t),F(Q。下料闸门关闭时尚在半空中的物料△G(留空量)会影响参数G(t),使测量值小于真实重量值，物料下落的冲击力F。)，会使测量值大于真实重量值。针对这两个关键误差来源，设计了三级下料系统并加入了基于模糊控制的PID算法。

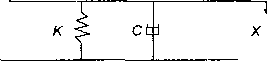
图1称重系统模型

2三料速下料系统
好的动态系统，关键就是在保证称重速度的同时，能够具有很高的称重精度。三料速下料系统就在于保证降低物料下落的冲击力FU)带来的误差影响的同时，又有效地保证了称重效率。
三料速系统主要是在下料结构上设计三级闸门(大投、中投、小投)，基于时间对闸门的开、合状态进行流程控制。其基本工作过程如下：①启动，同时开启大投、中投、小投，快速卸料；②当物料的称重值大于大投设定值时，关闭大投，进行中速卸料,并等待4时间(用于避免过冲)；③继续卸料，当物料的称重值大于中投设定值时，关闭中投，进行慢速卸料,并且等待4时间(用于避免过冲)；④当物料的称重值大于目标设定值时，关闭小投，停止卸料,并等待Z2时间(用于避免计量斗振动)；⑤如时间到后，等待打开夹带信
号，如果打开夹带信号到了,就将物料卸入包装袋，如果打开夹带信号没到，则等待夹带信号；⑥卸料过程中，当称重小于等于零区值时，延时為时间后关闭卸料信号，同时开启爲和以定时器上时间到后则关闭夹带信号,松开包装袋；⑦机时间到后则启动下一次称重过程。自动控制信号的时序图见图2。

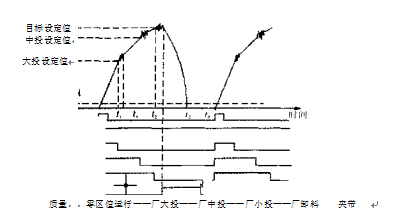
图2三料速控制信号时序图
其中大投设定值、中投设定值、目标设定值、零区值及各种时间参数均可以由用户根据现场实际工作情况进行手动设定，以满足实际包装的精度和速度要求。手动设定的数据可以在控制器中存储，每一组数据参数称为一个配方。同时，也可以根据现场实际的需要，预先将8个常用配方(根据现场情况实验得出)存于控制器内，当包装的目标值发生变化或者包装的物料不同时，直接靠程序载人相应的配方即可，不再需要手工设定每个参数。在整个控制过程中，大投和中投的关闭主要是决定称重速率问题，小投的关闭主要是决定称重的精度问题(有效控制了前面系统模型中Gh)和F(z)参数)。
定时器作用说明
大投和中投关闭后，避免过冲，系统停止采样时间.如判定秤体抖动时间。计量斗中物料卸料完后，卸料门延时开时间。避免卸料如不净，延时4后关闭卸料门。
两个称重过程的间隔时间。为了进一步避免秤体抖动,延时后开始下一次称重过程。松包装袋延时时间。卸料门关闭后。延时后才关闭夹带信号，松开包装带。
注设定时间范围均为。〜99s
3误差的动态校正
3.1算法的推导
在定量动态称重过程中，存在着系统带来的许多干扰，如称重抖动、物料的留空量△&、物料下落的冲击力F(Q、机械结构的动作滞后等，在加入了三料速控制系统后也不能完全消除，因此，只有进一步利用控制算法进行一定程度的消除，以达到所要求的精度。笔者采用基于数字增量式的PID控制算法，对称重过程中产生的干扰进行误差动态校正。
PID算法是根据微控制器对传感器釆样时刻的偏差值进行计算控制，其特点是加入了比例、积分、微分算法，能够有效而快速地调节系统偏差，消除稳态误差，进一步提高系统的响应速度和稳定性。PID控制器的理想算法⑶如下：
u(t)=Kp[e(t)+^^e(t)dt+Td^-3(1)其中，比例环节通过参数Kp控制，Kp越大比例环节越明显，但过大的Kp会造成很大的超调量，影响系统稳定性；积分环节通过参数T.控制，T,越大积分环节效果越明显，但积分环节的引入会使系统稳定性下降，动态响应变慢；微分环节通过参数Td控制，R越大微分环节效果越明显，调节适当的微分环节可以有效地减少超调量和调节时间，微分环节也会放大噪声信号，因此也不能过分增加。
数字增量式PID是指将积分项和微分项进行离散处理，每次输出控制量的增量。具体处理如下：以T为采样周期，K为采样序号，则离散化的釆样时间KT就对应连续时间用求和的形式代表积分，用增量的形式代替微分，算法变换如下⑴：
7QkT(k=0,1,2,3    )
＜財)&0応5)=丁多，⑵些§    =色_心
Idt    T    T
将式(2)带入式(1),则离散的PID控制器表达式为：
k
ut=Kg+Kt    +Ki(ek—    )+u0(3)
式中成为采样序列§"=0,1,2,3……;uk为第互次采样时刻控制器的采样值；4为第&次釆样时刻的输入偏差值为第k~l次釆样时刻的输入偏T差值;M为比例系数，K,为积分系数,Kj=KpKd为微分系数,Kd=Kp学，“。为开始进行PID控制时控制器采集到的初始量。其中如果采样周期(T)足够小，得到的近似结果就能获得足够的精确度，此时，离散的和连续的PID算法将十分接近⑶。我们使用的A/D最高采样频率能达到200kHz,能具有足够小的采样周期。
根据递推原理，由式(3)可以得到：
Zko=Kp(ek—境--1)+Kxek+KA(ek—2e^x—ek-2)
=Kp△玖+Kiek+Kd(△《一    )    (4)式中，e-i—e-2,则式(4)即为数字增量式PID控制算法，整理后有：
△g=Aek+Ri+Cek-2    (5)
式中，A=Kp(l+£+¥),B=—Kp(l+^),C=珞％其中的未知参数均为与釆样周期、比例增益、积分时间常数和微分时间常数有关的参数。
3.2算法的控制程序流程(图3)

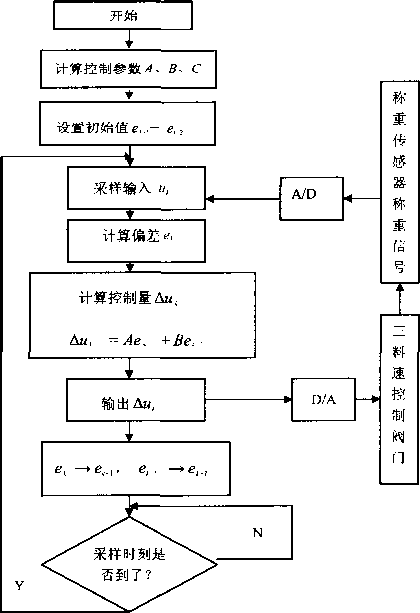
图3数字增量式PID算法实现流程
4样机的试验结果
系统设计技术指标：称重计量精度，小于±0.2%；称重范围，20〜50kg；包装速度，15包/min。
在样机上对大豆进行称重计量实验，重量目标设定值为25kg,设定控制器参数见表2〜表3,记录每次称重的实际重量值，误差值为实际重量值与设定值的差。

使用不同的PID控制参数：试验1,A=3.446,B=-5.72,C=1.224；试验2,A=3.377,B=-3.818,C=1.079；试验3,A=3.484,B=—4.298(=1.326。试验结果见表4。
表3实验样机对三料速控制过程中重量值的设置

由表4可得出，加入了三料速系统和数字增量式PID算法后，系统能够很好地调节称重误差，计量精度可达0.16%，在试验中完全能满足样机对农用化肥定量包装的称重精度。有效的调节PID算法中的参数厶、B、C,能够得到比较稳定的系统，参数A、B、C之间应该协调选取。
5结论
通过对动态称重系统进行建模分析，找出关键性误差来源，加入了三料速控制系统和基于数字增量式PID的控制算法。通过样机对大豆的称重实验数据，可以看出本系统在保证称重速度的同时，能够达到很高的精度。

文章来源于网络转载，侵删